ll numero 72 nel libro "La Smorfia" viene associato "a maraviglia" (lo stupore) e tale associazione tra numero e rappresentazione simbolica viene impiegato, nella cabbalah napoletana, per interpretare sogni ed eventi inspiegabili, per poi giocarne le combinazioni al lotto.
Meraviglia e stupore crea anche il mistero del numero 72 della Gioconda di Leonardo da Vinci
ll numero '72', che si intravede sotto l'arcata del ponte dipinto da Leonardo da Vinci alla sinistra della
'Gioconda', è stato individuato da Silvano Vinceti, presidente del Comitato Nazionale per la Valorizzazione dei Beni Storici e Culturali, e sembrerebbe riferirsi alla distruzione del Ponte Gobbo di Bobbio (Piacenza) avvenuta nel 1472 per la piena del Trebbia.
Ne da conferma anche la studiosa savonese Carla Glori che identifica nella Gioconda, Bianca Giovanna
Sforza e localizza nello splendido borgo piacentino di Bobbio, il paesaggio che fa da sfondo al celebre ritratto leonardesco.
Gli studi di Carla Glori, raccolti nel libro 'Enigma Leonardo: la Gioconda, in memoria di Bianca', dimostrano come Leonardo "ha apposto il numero '72' sotto l'arcata del ponte Gobbo per ricordare quella devastante piena del Trebbia e probabilmente per far sì che qualcuno identificasse l'emblematico ponte ed il luogo che fa da sfondo alla Gioconda".
Il trattato della studiosa savonese, inviato al Departement des Peintures del Museo francese del Louvre (dov'é custodita la Gioconda) per i riscontri, è stato ripreso anche da importanti quotidiani stranieri, tra cui il Daily Mail e il Guardian. (http://www.ilpiacenza.it/eventi/arte-gioconda-bobbio-giornali-inglesi.html)
Il trattato della studiosa savonese, inviato al Departement des Peintures del Museo francese del Louvre (dov'é custodita la Gioconda) per i riscontri, è stato ripreso anche da importanti quotidiani stranieri, tra cui il Daily Mail e il Guardian. (http://www.ilpiacenza.it/eventi/arte-gioconda-bobbio-giornali-inglesi.html)
Ancora meraviglia e stupore crea il "72" nella Bibbia
La Cabbalah cristiana che si diffuse notevolmente nel Rinascimento, anche grazie al contributo di Pico della
La Cabbalah cristiana che si diffuse notevolmente nel Rinascimento, anche grazie al contributo di Pico della
Mirandola, come la Cabbalah ebraica, ha attinto tutti i propri insegnamenti dalla Torah e dallo Zoahr, il Libro
dello Splendore, ma da dove si originano i 72 Nomi di Dio, che nella Cabbalah cristiana danno nome alle 72
energie definite come "angeli custodi"?
Nel Libro dell'Esodo la scrittura ha una forma unica, che non si ripete in nessun altro punto della Bibbia: 3
versetti consecutivi (Esodo 14, dal 19 al 21) sono formati da 72 lettere ciascuno; si tratta di quelli che narrano il momento culminante dell'intervento divino, l'aprirsi delle acque del Mar Rosso:
(19) L'angelo di Dio, che precedeva l'accampamento d'Israele, cambiò posto e passò indietro. Anche la colonna di nube si mosse e dal davanti passò indietro.
(20) Venne così a trovarsi tra l'accampamento degli Egiziani e quello d'Israele. Ora la nube era tenebrosa per gli uni, mentre per gli altri illuminava la notte; così gli uni non poterono avvicinarsi agli altri durante tutta la notte.
(21) Allora Mosè stese la mano sul mare. E il Signore, durante tutta la notte, sospinse il mare con un forte vento d'oriente, rendendolo asciutto; le acque si divisero.
- 72 è anche il valore numerico della parola Hesed (o Chesed), che esprime la misercordia dell'amore o la grazia (e nelle sfere angeliche corrisponde al Coro delle Dominazioni, gli angeli governati dall'Arcangelo Hesediel).
- 72 sono anche i gradini della scala vista in sogno da Giacobbe, tramite la quale gli angeli scendono e salgono dalla terra al Cielo.
Da questi tre versetti è derivata la "tecnologia" spirituale che ha dato forma ai 72 Santi Nomi di Dio, costituiti
ciascuno da tre lettere, ognuna delle quali è presa da uno dei 3 versi: il primo Nome è formato dalla prima
lettera del primo verso, l'ultima del secondo e la prima del terzo. Il secondo Nome dalla seconda lettera del
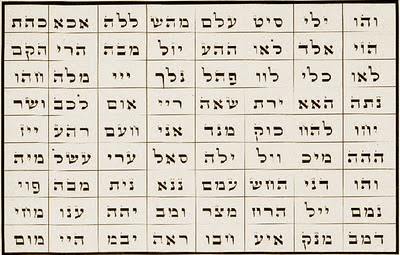
primo versetto, la penultima del secondo e la seconda del terzo.. e così via fino a formare 72 trigrammi, cioè 72 radici di 3 lettere, quelle che si vedono nella tabella. (http://tuttigliangeli.blogspot.it/p/i-72-nomi-di-dio-angeli-edemoni.html)
Infine vediamo "a maraviglia" di alcune delle proprietà matematiche del nostro numero 72
- 72 è il numero dei discepoli scelti da Gesù secondo alcuni manoscritti di Luca 10,1 e Luca 10,17. Altri manoscritti degli stessi versetti parlano di 70 discepoli.
- 72 é il numero totale di libri nella Sacra Bibbia nella versione cattolica se si considera il libro delle Lamentazioni come parte del libro di Geremia.
- 72 è il numero totale degli articoli del codice dei templari
- È un numero composto, (ovvero non è primo), con i seguenti 12 divisori: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18,24 e 36
- È un numero abbondante poiché minore della somma dei relativi divisori (escludendo se stesso è 139)
Un numero abbondante è un numero naturale minore della somma dei suoi divisori interi (escludendo sé stesso). La sequenza dei numeri abbondanti comincia così: (Sequenza A005101 della OEIS-On-Line Encyclopedia of Integer Sequences)
12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, 126, 132, 138, 140, 144, 150, 156, 160, 162, 168, 174, 176, 180, 186, 192, 196, 198, 200, 204, 208, 210, 216, 220, 222, 224, 228, 234, 240, 246, 252, 258, 260, 264, 270...
Una curiosità è data dal fatto che il primo numero naturale abbondante dispari è 945 e che tutti i multipli interi dei numeri abbondanti e perfetti sono a loro volta numeri abbondanti e perfetti
Una curiosità è data dal fatto che il primo numero naturale abbondante dispari è 945 e che tutti i multipli interi dei numeri abbondanti e perfetti sono a loro volta numeri abbondanti e perfetti
- È un numero altamente totiente con più soluzioni all'equazione φ(x) = n che qualsiasi numero più basso.
In teoria dei numeri, un numero altamente totiente è un intero k maggiore di 1 tale che l'equazione φ(x) = n, dove φ rappresenta la funzione totiente di Eulero, abbia più soluzioni che qualsiasi altro numero minore di n.
I primi numeri altamente totienti sono:
1, 2, 4, 8, 12, 24, 48, 72, 144, 240, 432, 480,576, 720, 1152, 1440
- È un numero idoneo.
I numeri idonei sono stati studiati da Leonhard Eulero e Carl Friedrich Gauss che trovarono 65 numeri idonei: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, 33, 37, 40, 42, 45, 48, 57, 58, 60, 70, 72, 78, 85, 88, 93, 102, 105, 112, 120, 130, 133, 165, 168, 177, 190, 210, 232, 240, 253, 273, 280, 312, 330, 345, 357, 385, 408, 462, 520, 760, 840, 1320, 1365 e 1848.
I due matematici congetturarono che questi fossero gli unici numeri idonei esistenti. Nel 1973 Weinberger ha dimostrato che ne esiste al più un altro.
- È un numero di Ulam.
In teoria dei numeri, una successione di Ulam è una sequenza di numeri interi tale che ogni suo membro sia esprimibile, in uno e un solo modo, come somma di due membri precedenti e distinti della successione
72=69+3
I primi termini della successione di Ulam (1, 2), ovvero i primi numeri di Ulam sono:
1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53, 57, 62, 69, 72, 77, 82, 87, 97, 99, 102, 106, 114
1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53, 57, 62, 69, 72, 77, 82, 87, 97, 99, 102, 106, 114
- È la somma di quattro numeri primi consecutivi:
72 = 13 + 17 + 19 + 23
- È la somma di sei numeri primi consecutivi:
72 = 5 + 7 + 11 + 13 + 17 + 19
- È un numero di Harshad.
Un numero di Harshad in una data base è un numero intero positivo divisibile per la somma delle proprie cifre.
La definizione dei numeri di Harshad è stata data dal matematico indiano Dattatreya Ramachandra Kaprekar. Il termine Harshad deriva dal sanscrito "har a" che significa "grande gioia". A volte ci si riferisce a questi numeri anche come numeri di Niven, in onore del matematico
72 è divisibile per 9 (7+2)
72 è divisibile per 9 (7+2)
- È un numero potente.
Un numero potente è il prodotto di un quadrato per un cubo, ovvero può essere scomposto nella forma m = a^2*b^3, dove a e b sono interi positivi (eventualmente uguali a 1)
72 = 3^2 * 2^3
- È la somma di due quadrati,
72 = 6^2 + 6^2.
- Può essere rappresentato, in 3 modi diversi, come differenza tra 2 quadrati:
72=9^2 - 3^2,
72=11^2 - 7^2
72=19^2 - 17^2
Quello che i Pitagorici chiamavano invece propriamente un gnomone (parola che in origine a Babilonia denotava un bastone piantato verticalmente la cui ombra era usata per misurare il tempo, per i Pitagorici era la squadra da falegname), si ottiene sottraendo da un quadrato il quadrato immediatamente precedente, in simboli:
(n + 1)^2 - n^2 = 2n + 1
- È un numero rifattorizzabile, essendo divisibile per il numero dei suoi divisori.
I suoi divisori sono 12 e 72:12= 6
Bibliografia
G. Frei, Euler's convenient numbers, Math. Intell. Vol. 7 N° 3 (1985), 55 58 e 64.
P. Weinberger, Exponents of the class groups of complex quadratic fields, Acta Arith., 22 (1973), 117 124.
H. G. Grundmann, Sequences of consecutive Niven numbers, Fibonacci Quarterly 32 (1994), 174-175
McDaniel, Wayne L. (1982). Representations of every integer as the difference of powerful numbers. Fibonacci Quarterly 20: 85 87.
S. Colton, "Refactorable Numbers - A Machine Invention," Journal of Integer Sequences, Vol. 2 (1999), Article 99.1.2



Nessun commento:
Posta un commento